Algebraic immunity of Boolean functions

Algebraic immunity of Boolean functions

In 2003, the discovery of algebraic immunity and annihilators have significantly impacted cryptanalysis by shaping how cryptographers approach the design of secure Boolean functions used in stream ciphers. These concepts have now become integral in defending against algebraic attacks. In fact, to achieve optimum resistance against those, cryptographers had to generally increase the number of variables in their constructions and choose functions with as high algebraic immunity as possible.

Among impacted designs was the filter generator, a technique used to break linearity in most LFSR-based stream ciphers by simply filtering the output of an LFSR through a highly non-linear boolean function. The concept of algebraic immunity shook it to its core as it appears a function with all previously required properties (nonlinearity, balancedness and resistance to fast algebraic attacks) in addition to great algebraic immunity was nowhere to be found until 2008 where an infinite class of such function possessing all mandatory features has been discovered.

Algebraic immunity and annihilators

The algebraic immunity of a function [math]\displaystyle{ AI(f) }[/math] measures its resistance to algebraic attacks. Specifically it refers to the minimum algebraic degree of a non-zero Boolean function (called the annihilator of [math]\displaystyle{ f }[/math]) that annihilates [math]\displaystyle{ f }[/math] or its complement.

Formally, let [math]\displaystyle{ f: \mathbb{F}_2^n \rightarrow \mathbb{F}_2 }[/math] be a Boolean function. An annihilator of [math]\displaystyle{ f }[/math] or [math]\displaystyle{ f \oplus 1 }[/math] is a non-zero Boolean function [math]\displaystyle{ g: \mathbb{F}_2^n \rightarrow \mathbb{F}_2 }[/math] such that [math]\displaystyle{ fg = 0 }[/math].

The algebraic immunity of a boolean function is defined as the minimum algebraic degree among its annihilators [math]\displaystyle{ AI(f) = \min(d^\circ (g) \mid g \in An(f)) }[/math].

For all Boolean functions, the algebraic immunity is bounded by [math]\displaystyle{ AI(f) \leq \min(d^\circ(f), \lceil\frac{n}{2}\rceil) }[/math].

Example through code

Boolean functions are defined within Sagemath by importing the sage.crypto.boolean_function module and its components which are not loaded by default. With Sagemath a Boolean function can be created from its truth table or from a Boolean polynomial. The example below illustrates the latter.

sage: from sage.crypto.boolean_function import BooleanFunction
sage: B.<x0, x1, x2, x3> = BooleanPolynomialRing(4)
sage: f = x0*x1*x2*x3 + x0*x2*x3 + x1*x2*x3 + x0*x1 + x0*x3 + x1*x2 + x3 + 1
sage: F = BooleanFunction(f)
sage: F.algebraic_degree()
4

It is possible to compute an annihilator of F which algebraic degree is equal to [math]\displaystyle{ AI(f) }[/math]. Note that [math]\displaystyle{ d^\circ(f) = 4 }[/math] but [math]\displaystyle{ AI(f) = 2 = \lceil\frac{n}{2}\rceil }[/math] and [math]\displaystyle{ f }[/math] has optimal algebraic immunity in this example.

sage: AI, g = F.algebraic_immunity(annihilator=True)
sage: AI
2
sage: g
x0*x3 + x3
sage: f * g == 0
True

Characterization of annihilators by the Walsh transform

If [math]\displaystyle{ g }[/math] is an annihilator of [math]\displaystyle{ f }[/math], then [math]\displaystyle{ f }[/math] and [math]\displaystyle{ g }[/math] must be orthogonal functions over [math]\displaystyle{ F_2^n }[/math]. This orthogonality property can be visualized through the Walsh coefficients of both functions.

Recall that for any two Boolean functions [math]\displaystyle{ f }[/math] and [math]\displaystyle{ g }[/math], the integer addition is defined as [math]\displaystyle{ f + g = f \oplus g + 2fg }[/math]. However [math]\displaystyle{ g \in An(f) }[/math] so this reduces to [math]\displaystyle{ f + g = f \oplus g }[/math] or the classical field addition. This reduction through annihilators directly leads to the following formula

[math]\displaystyle{ g \in An(f) \iff \forall a \neq 0, W_{f \oplus g}(a) = W_f(a) + W_g(a) }[/math]

that generalizes for all [math]\displaystyle{ a }[/math] as

[math]\displaystyle{ g \in An(f) \iff \forall a \in \mathbb{F}_2^n, W_{f \oplus g}(a) + 2^n \delta_0(a) = W_f(a) + W_g(a), }[/math]

with [math]\displaystyle{ \delta(a) = \sum_{x \in \mathbb{F}_2^n} (-1)^{a\cdot x} }[/math].

Example through code

Recalling previously defined variables, the walsh coefficients can be directly computed as a list.

sage: _, g = F.algebraic_immunity(annihilator=True)
sage: G = BooleanFunction(g)
sage: F_plus_G = BooleanFunction(f + g)
sage: wf = F.walsh_hadamard_transform()
sage: wg = G.walsh_hadamard_transform()
sage: wfg = F_plus_G.walsh_hadamard_transform()

And verify that the equation holds.

sage: n = F.nvariables()
sage: for a in range(1, 2^n):
....:     assert wfg[a] == wf[a] + wg[a]

Perfect algebraic immune functions

A perfect algebraic immune function is a Boolean function [math]\displaystyle{ f: \mathbb{F}_2^n \rightarrow \mathbb{F}_2 }[/math] such that for any pair of strictly positive integers [math]\displaystyle{ (e, d) }[/math] where [math]\displaystyle{ e + d \lt n }[/math] and [math]\displaystyle{ e \lt \frac{n}{2} }[/math], there is no Boolean function [math]\displaystyle{ g }[/math] that satisfies [math]\displaystyle{ d^\circ(g) \leq e }[/math] and [math]\displaystyle{ d^\circ(fg) \leq d }[/math].

The conditions on [math]\displaystyle{ (e, d) }[/math] are designed to restrict the potential space of attack functions [math]\displaystyle{ g }[/math] making it more difficult to reduce the complexity of the function [math]\displaystyle{ f }[/math] using algebraic methods. This criteria makes perfect algebraic immunity a highly desirable property in the construction of stream ciphers.

Balanced perfect algebraic immune functions can exist only if [math]\displaystyle{ n }[/math] is equal to 1 plus a power of 2. Unbalanced perfect algebraic immune functions exist only if [math]\displaystyle{ n }[/math] is a power of 2.

Consequences of algebraic attacks on the design of stream ciphers

A difference by 1 in the algebraic immunity of a function [math]\displaystyle{ f }[/math], used as combiner or filter in a stream cipher, makes a big difference in the efficiency of algebraic attacks. The designer needs then to choose [math]\displaystyle{ f }[/math] with optimal or near-optimal algebraic immunity. Ideally, one would choose a perfectly algebraic immune function, but finding such functions that also satisfy other key properties, like nonlinearity or balancedness, is not straightforward.

Let [math]\displaystyle{ f }[/math] be an [math]\displaystyle{ n }[/math]-variable Boolean function with algebraic immunity [math]\displaystyle{ \lceil\frac{n}{2}\rceil }[/math] used to filter an LFSR of length [math]\displaystyle{ N \geq 2k }[/math] where [math]\displaystyle{ k }[/math] is the length of the key. The time complexity of an attack using an annihilator of degree [math]\displaystyle{ \lceil\frac{n}{2}\rceil }[/math], where realistic parameters involve [math]\displaystyle{ N = 256 }[/math] and [math]\displaystyle{ k = 128 }[/math], would be roughly [math]\displaystyle{ 2^{80} }[/math].

However, if the attacker knows several linearly independent annihilators with said degree, then the number of variables must be increased to approximately 20 in practice. This impacts the computational efficiency of stream ciphers that used to deal with at most 10 variables Boolean functions before.

Combining high algebraic immunity with high nonlinearity

Boolean functions for building stream ciphers are chosen to allow resistance to all known attacks and possibly to be computable as fast as possible. In that sense, finding a function achieving optimal or almost-optimal algebraic immunity and high nonlinearity remains a challenge.

Many studies had been carried out to seek for the best functions class that would ensure both properties but eventually led to one of the parameters being too low for cryptographic purposes. Hence the need for design in an infinite class of functions achieving all the necessary criteria remained open until a work from Carlet and Feng in 2008.

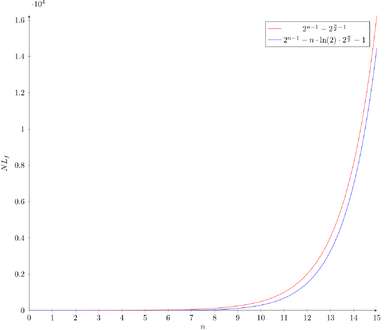
The primary construction of this class defines functions over [math]\displaystyle{ \mathbb{F}_{2^n} }[/math]. For any integer [math]\displaystyle{ s }[/math] and any primitive element [math]\displaystyle{ \alpha }[/math] of [math]\displaystyle{ \mathbb{F}_{2^n} }[/math], all balanced Boolean functions whose support is [math]\displaystyle{ \{\alpha^s, \ldots, \alpha^{2^{n-1} + s - 1}\} }[/math] have optimal algebraic [math]\displaystyle{ \lceil\frac{n}{2}\rceil }[/math]. Their nonlinearity is also suitable for cryptographic purposes and a lower bound is [math]\displaystyle{ \mathcal{NL}_f \geq 2^{n-1} - n \cdot \ln{2} \cdot 2^{n/2} - 1 }[/math] that is asymptotically similar to the covering radius bound.

While this bound is insufficient to prove strong general resistance for [math]\displaystyle{ f }[/math], the nonlinearity has been exhaustively computed up to [math]\displaystyle{ n = 26 }[/math] and the results happen to be highly favorable and sufficient. The good resistance to fast algebraic attacks has also been proved for all [math]\displaystyle{ n }[/math]. Hence these functions gather all the properties needed to build filters in stream ciphers resistant to all the main attacks.

Applications of algebraic immunity to cryptanalysis

A new kind of attacks, called algebraic attacks, was introduced in 2003 by Courtois and Meier and has significantly changed the situation with Boolean functions in stream ciphers. These attacks aim to directly recover the key or the internal state of the system by solving a system of multivariate equations and are as efficient as [math]\displaystyle{ AI(f) }[/math] is small.

Algebraic attacks: using the annihilator to reduce the degree

Suppose the output [math]\displaystyle{ s_i }[/math] of a stream cipher (or its internal state) depends on some nonlinear function [math]\displaystyle{ f }[/math] of high algebraic degree with [math]\displaystyle{ n }[/math] variables. Expressing each output bit in terms of [math]\displaystyle{ f }[/math] offers a system of multivariate equations of high degree. There exists methods to solve such a system using Gröbner bases but the high algebraic degree of [math]\displaystyle{ f }[/math] makes this attack impractical and computationally too expensive for real-life scenarios.

However, it is possible to lower the cost of solving such a system by considering annihilators of [math]\displaystyle{ f }[/math]. Consider the first scenario and assume the existence of two functions [math]\displaystyle{ g }[/math] and [math]\displaystyle{ h }[/math] such that [math]\displaystyle{ fg = h }[/math] both of low algebraic degree and [math]\displaystyle{ g, h \neq 0 }[/math]. Then each output [math]\displaystyle{ f(x) = s_i }[/math] can be expressed as [math]\displaystyle{ fg = gs_i = h }[/math] regarding

[math]\displaystyle{ s_i = \begin{cases} 1 & \text{use the equation } g - h = 0, \\ 0 & \text{use the equation } h = 0, \end{cases} }[/math]

However, if [math]\displaystyle{ g }[/math] has high algebraic degree but [math]\displaystyle{ h }[/math] has low algebraic degree, we must consider the scenario above with one additional constraint on the choice of the equations;

[math]\displaystyle{ s_i = \begin{cases} 1 & —, \\ 0 & \text{use the equation } h = 0. \end{cases} }[/math]

If [math]\displaystyle{ g }[/math] has high algebraic degree then so will [math]\displaystyle{ g - h }[/math] thus this equation is discarded when [math]\displaystyle{ s_i = 1 }[/math].

In the third scenario, if [math]\displaystyle{ g }[/math] is an annihilator of [math]\displaystyle{ f }[/math], then [math]\displaystyle{ fg = 0 }[/math] and if

[math]\displaystyle{ s_i = \begin{cases} 1 & \text{use the equation } g = 0, \\ 0 & —. \end{cases} }[/math]

For the latter, if [math]\displaystyle{ g }[/math] is a non-zero function of low degree [math]\displaystyle{ d }[/math], then the equation [math]\displaystyle{ g = 0 }[/math] will carry the same degree [math]\displaystyle{ d }[/math] for each output [math]\displaystyle{ s_i = }[/math] meaning that given [math]\displaystyle{ m }[/math] keystream bits, an average of [math]\displaystyle{ m/2 }[/math] multivariate equations of degree [math]\displaystyle{ d }[/math] can be derived.

Gröbner bases

When as many as the required [math]\displaystyle{ O(\binom{n}{d}) }[/math] keystream bits are not available, the system of multivariate equations can be solved with Gröbner bases algorithms but at a consequential increased cost in computations.

Linearization

In practice if [math]\displaystyle{ h }[/math] and [math]\displaystyle{ g }[/math] have sufficiently low algebraic degree (i.e. if [math]\displaystyle{ f }[/math] has poor algebraic immunity), it is possible to linearize the system by considering each monomial as a unique variable. However, the number of variables grows exponentially in the algebraic degree of the annihilator and is equal to [math]\displaystyle{ D = \textstyle \sum_{i = 0}^{d^\circ(g)} \binom{n}{i} }[/math] and solving a system of linear equations via Gaussian elimination takes [math]\displaystyle{ O(D^\omega) }[/math] operations where [math]\displaystyle{ \omega \approx 3 }[/math] is the exponent of the Gaussian reduction.